It's Really All About the Math
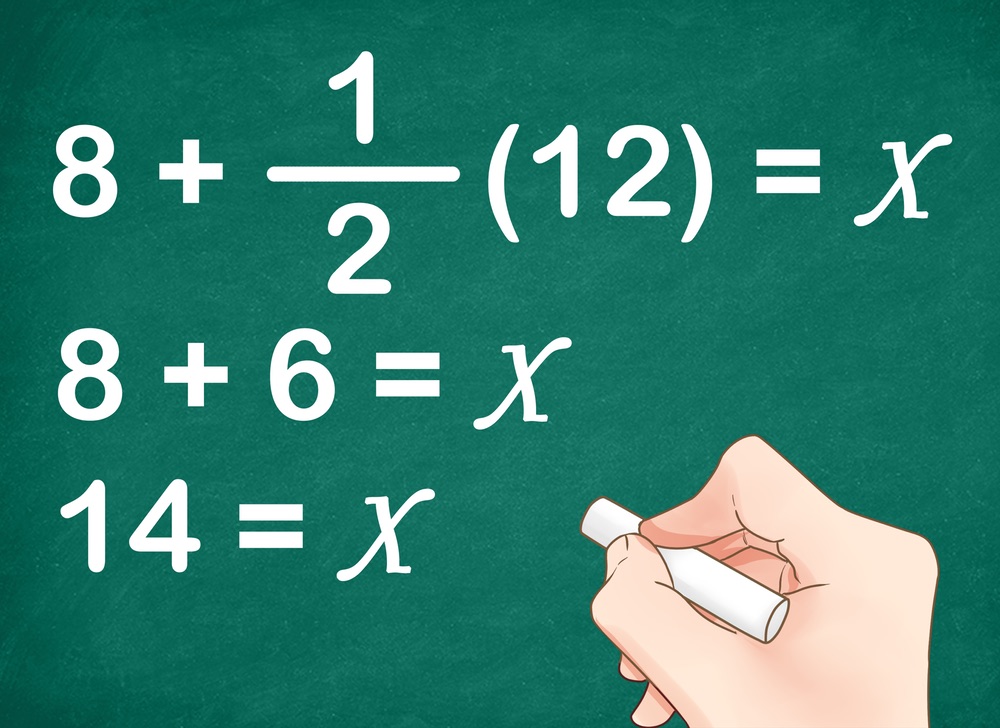
or
Bedskirts Exist for a Reason
So, I was making the bed the other day, and thought it would be nice to make a quilt. I had a picture in my mind of a cute kitty pattern in a rose print on a white background, with little ribbon bows. At first, I was going to design my own pattern, but then I thought it might be easier just to find one on the net. After some searching, I decided to go with this:

Now, one thing that has always bothered me about the comforters you buy is that it seems they're never big enough. So I wanted to measure this quilt so that it would cover all the pillows and the bolster, and be long and wide enough to reach to the floor. I worked out all the calculations for how many squares I would need, what the spacing should be, how wide the borders ought to be, etc. But then it occurred to me that there was one flaw in my calculations: corners.

If you have a rectangular bedspread, the corners are going to hang in a diamond-shape, and will drop down below the bottom edge of the quilt, as shown on the right. So, if the quilt edges reach all the way to the floor, the corners are going to drag on the ground, and, potentially, get stepped on and tripped over, and just generally be in the way. So how long can you make the quilt, and still keep the corners off the ground?
Well, if you stretch out the corner, you'll see that you have a right triangle.
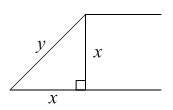
The diagonal line is the part that hangs down. So, if you look at the diagram on the left, y would be the distance from the top of the bed to the floor, if the corner were to just touch the ground. (You could probably even add an inch for loft.) x is the distance that the quilt overhangs the edge of the bed, which is what we want to determine. Applying the Pythagorean Theorem (a2 + b2 = c2), we know that in this case 2x2 = y2; solving for x, we get
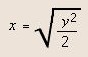
(You know, there ought to be a way to better render square roots and mathematical formulas with HTML!) So, since my bed is 27" high (I have bed risers to increase storage space), I know that I can make my quilt overhang the edge of the bed by about 19". And, it appears that the bedskirt is, after all, necessary, to cover the remaining gap.
Now I need to go back and recalculate my quilt dimensions.



